異なるn 個のデータが昇順に整列された表がある。 この表をm 個のデータごとのブロックに分割し、各ブロックの最後尾のデータだけを線形探索することによって、目的のデータの存在するブロックを探し出す。 次に、当該ブロック内を線形探索して目的のデータを探し出す。 この時の平均比較回数を表す式はどれか。 ここで、m は十分に大きく、n はm の倍数とし、目的のデータは必ず表の中に存在するものとする。
| ア |  |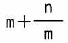
イ |  |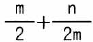
ウ |  |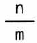
エ |  |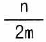
答え イ
【解説】
x 個のデータを線形探索したときの比較回数は x /2 である。
したがって、問題の方法を行った場合、m 個ブロックのどれに目的のデータがあるかの探索には m /2 回の比較が必要である。
さらに、各ブロックのデータの数はn /m 個であり、この中から目的のデータがあるかの探索には n /2m 回の比較が必要なので、合計で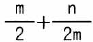回(イ)になる。
【キーワード】
・線形探索法
- 線形探索法
データの状態にかかわらず採用することができる探索方法で、探索するデータの先頭から順に、探索する値と一致するかを比較していきます。
整列済み、未整列にかかわらず探索可能ですが、整列済みのデータの場合は2分探索法に比べ時間がかかります。
もっと、「線形探索」について調べてみよう。
戻る
一覧へ
次へ