配列A[1]、A[2]、…、A[n ]でA[1]を根とし、A[i ]の左側の子をA[2i ]、右側の子をA[2i +1]とみなすことによって、2分木を表現する。
このとき、配列を先頭から順に調べて行くことは、2分木の探索のどれに当たるか。
| ア | 行きがけ順(先行順)深さ優先探索 |
| イ | 帰りがけ順(後行順)深さ優先探索 |
| ウ | 通りがけ順(中間順)深さ優先探索 |
| エ | 幅優先探索 |
答え エ
【解説】
2分木の探索で、配列の順に探索する方法(2分木図では、根→2段目の節全部→3段目の節全部→4段目の節全部(1→2→3→4→5→6→7→8→9→10→11→12→13→14→15)と探索していく方法)は幅優先探索(エ)といいます。
2分木の深さ優先探索を図で表すと下のようになります。
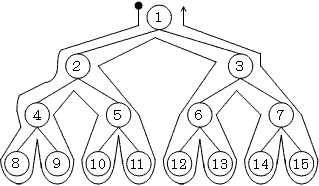
| ア | 行きがけ順(先行順)深さ優先探索では、1→2→4→8→9→5→10→11→3→6→12→12→7→14→15 という探索順になります。 図では探索の線が節の左を通るときその節を探索します。 |
| イ | 帰りがけ順(後行順)深さ優先探索では、8→9→4→10→11→5→2→12→13→6→14→15→7→3→1 という探索順になります。 図では探索の線が節の右を通るときその節を探索します。 |
| ウ | 通りがけ順(中間順)深さ優先探索では、8→4→9→2→10→5→11→1→12→6→13→3→14→7→15 という探索順になります。 図では探索の線が節の下を通るときその節を探索します。 |
【キーワード】
・探索順
- 探索順
問題で書かれた2分木を図にすると、下のようになる。A 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 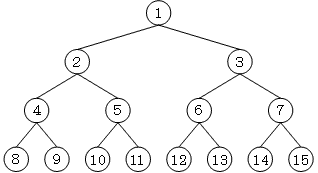
2分木の探索としては、配列の順に探索する方法と、2分木の図の親子の関係に沿って探索する方法があります。
もっと、「探索順」について調べてみよう。
 戻る
戻る 一覧へ
一覧へ 次へ
次へ