四つの整数を引数とする関数d(X1, Y1, X2, Y2)を、次のとおりに定義する。
d(X1, Y1, X2, Y2) = | X1 - X2 | + | Y1 - Y2 |
この関数は、2点(X1, Y1)と(X2, Y2)との間の2次元正方格子上の最短経路長を求めるものである。
その性質に関する記述のうち、適切なものはどれか。
| [例] | 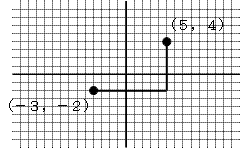 |
d(-3, -2, 5, 4) = 8 + 6 = 14 |
| ア | d(0, 0, X2, Y2) ≤ 1を満たす整数の組(X2, Y2)は、全部で四つある。 |
| イ | d(2X1, 2Y1, 2X2, 2Y2) = 4d(X1, Y1, X2, Y2)である。 |
| ウ | d(X1, Y1, X2, Y2) = 0 ならば、X1 = X2 = Y1 = Y2である。 |
| エ | d(X1, Y1, X2, Y2) = d(Y2, X2, Y1, X1) |
答え エ
【解説】
| ア | (0, 0)からの距離が1未満の組は(1, 0)、(0, 1)、(-1, 0)、(0, -1)、(0, 0)の5個ある。 |
| イ | 例として、d(1, 1, 2, 2) = 2 で、d(2×1, 2×1, 2×2, 2×2) = d(2, 2, 4, 4) = 4 なので、設問の式は成立しない。 |
| ウ | d(X1, Y1, X2, Y2) = 0 で、あるためには、(X1, Y1)と(X2, Y2)が同じであればいいので、X1 = X2 かつ Y1 = Y2 であればよい。 |
| エ | 設問の式の左辺は d(X1, Y1, X2, Y2) = | X1 - X2 | + | Y1 - Y2 | であり、右辺は d(Y2, X2, Y1, X1) = | Y2 - Y1 | + | X2 - X1 | で、| X1 - X2 | = | X2 - X1 | であり、| Y1 - Y2 | = | Y2-Y1 | であるので、設問の式は成立する。 |
【キーワード】
・最短経路探索
- 最短経路探索
地点Sから地点Gへの移動距離を最も小さくする経路を探す方法です。
問題の2次元正方格子上の場合は、各交差点からの移動は縦・横の移動しかなく(図の線の上しか移動できない。)、各交差点間の移動距離は1である。
もっと、「最短経路探索」について調べてみよう。
 戻る
戻る 一覧へ
一覧へ 次へ
次へ