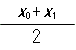 とする。
とする。0≤x ≤1の範囲で単調に増加する連続関数f (x )がf (0)≤0≤f (1)を満たすときに、区間内でf (x ) = 0であるx の値を近似的に求めるアルゴリズムにおいて、(2)は何回実行されるか。
| [アルゴリズム] | |
| (1) | x0←0、x1←1とする。 |
| (2) | x ←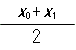 とする。 とする。 |
| (3) | x1 - x <0.001ならばx の値を近似値として終了する。 |
| (4) | f (x )≥0ならばx1←x として、そうでなければx0←x とする。 |
| (5) | (2)に戻る。 |
| ア | 10 |
| イ | 20 |
| ウ | 100 |
| エ | 1,000 |
答え ア
【解説】
x ←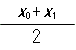 は、x0とx1の中間値を求める計算で、このx とx1の差が0.001未満になるまで計算するので、回数を考えると
は、x0とx1の中間値を求める計算で、このx とx1の差が0.001未満になるまで計算するので、回数を考えると
【キーワード】
・アルゴリズム